L’alumnat del taller d’aprofundiment Més mates lúdiques de 2n d’ESO volem compartir amb tots vosaltres els sabers bàsics que hem après durant la primera avaluació.
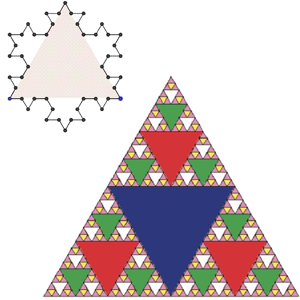
Per això, hem construït un arbre de Nadal amb llaunes de coca-cola buides. L’arbre és un fractal anomenat triangle de Sierpinski i es construeix fraccionant un triangle equilàter de la següent manera:

Es busquen els punts mitjans dels tres costats del triangle equilàter i s’uneixen entre ells. D’aquesta manera, el triangle inicial queda dividit en quatre triangles també equilàters. El triangle del centre es queda buit i el procediment anterior es repeteix amb cadascun dels tres triangles dels extrems.
I aquest procediment el repetim tantes vegades com vulguem.
Com podem saber quantes llaunes de Coca-Cola hem utilitzat per construir l’arbre de Nadal sense necessitat de comptar-les?
Molt fàcil!
Cada vegada que repetim el procediment, deixem un triangle buit i ens quedem amb tres triangles. I aquest procediment el repetim cinc vegades. Si elevem el nombre de triangles al nombre de vegades, obtenim el nombre de llaunes utilitzades, 35 = 243 llaunes.
I L’ESTRELLA DE NADAL TAMBÉ ÉS UN FRACTAL?
Doncs sí, l’estrella de Nadal que hem construït és un fractal anomenat floc de neu de Koch i es construeix fraccionant els tres costats d’un triangle equilàter de la següent manera:

Cada costat es divideix en tres segments de la mateixa longitud. El segment del centre s’elimina i es substitueix per dos segments de la mateixa longitud que el segment eliminat i que formen un angle de 60º amb aquest. D’aquesta manera, cada costat es transforma en quatre segments iguals i el procediment anterior es repeteix amb cadascun d’aquests quatre segments.
I aquest procediment el repetim tantes vegades com vulguem amb els tres costats del triangle equilàter.
L’estrella de Nadal està construïda sobre un triangle equilàter de 54 cm de costat. Com podem saber el perímetre d’aquesta estrella sense necessitat de mesurar un costat i multiplicar aquesta mesura pel nombre de costats que té?
Molt fàcil!
Cada costat el dividim en tres segments iguals, eliminem el segment del centre i afegim dos segments iguals més, amb la qual cosa cada costat té quatre segments. I aquest procediment el repetim dues vegades. Per tant, la longitud de cada costat és 54 ·(4/3)2 = 96 cm i com que l’estrella té tres costats, el perímetre de l’estrella és 96 · 3 = 288 cm.

BON NADAL I BON ANY NOU A TOTHOM!!
Pablo Jovaní Dpt. de Matemàtiques.