Las Matemáticas no es sólo esa asignatura que tanta preocupación provoca en alumnos, padres y profesores cada vez que iniciamos un curso. Llega septiembre, vemos los libros de texto y pensamos, esto es lo que quiero que hagan mis alumnos, operar, resolver problemas algebraicos, apreciar la geometría, sacar toda la información posible de un estudio estadístico…. Es verdad que, a veces, nosotros mismos las reducimos a eso y es este desarrollo formal de la asignatura el que nos deja casi sin tiempo para desarrollar un aspecto fundamental que es su componente lúdico. Los acertijos, pasatiempos, juegos de ingenio… siempre han estado presentes a lo largo de la historia y este carácter lúdico es el que en ocasiones ha impulsado el desarrollo de las Matemáticas.
Tengo una caja llena de animales:
Todos son gatos menos dos.
Todos son patos menos dos.
Todos son sapos menos dos.
¿Cuántos animales tengo en la caja?
Jugar es divertirse, pero divertirse cumpliendo unas reglas. Unas veces ganaremos y en otras ocasiones perderemos, lo importante es que en ambos casos podemos sacar ciertas conclusiones y buscar estrategias que nos ayuden la próxima vez. Con el juego podemos potenciar la creatividad, el ingenio, la capacidad de abstracción, la autoestima, la ilusión por las Matemáticas…etc.
En Matemáticas los juegos constituyen un problema, partimos de una situación inicial que se va modificando mediante acciones que nos llevan al objetivo, la victoria o solución del problema. Cada vez que tomamos una decisión se nos abren nuevas posibilidades, la complejidad del problema dependerá del número de combinaciones posibles que se pueden dar hasta llegar al objetivo.
Veamos algunos ejemplos que ilustran lo anterior y a la vez nos servirán para pasar un buen rato.
Para empezar, otro acertijo: ¿Cómo podemos colocar 9 bolas en 4 cajas de forma que cada caja tenga un número impar de bolas y distinto al de cada una de las otras tres?
Otro de números. Todos conocemos el juego del ajedrez, la leyenda sobre su origen y las reglas que hay que seguir para jugar. Pero, ¿cuántos cuadrados hay en un tablero de ajedrez?
“Cuadrados mágicos”. Un cuadrado mágico está dividido en n filas y n columnas formando n2 celdas que contienen todos los distintos números desde 1 hasta n2, de modo que sumándolos en vertical, horizontal y diagonal, siempre nos da el mismo resultado. Relacionados con los cuadrados mágicos están los sudokus en sus diferentes versiones
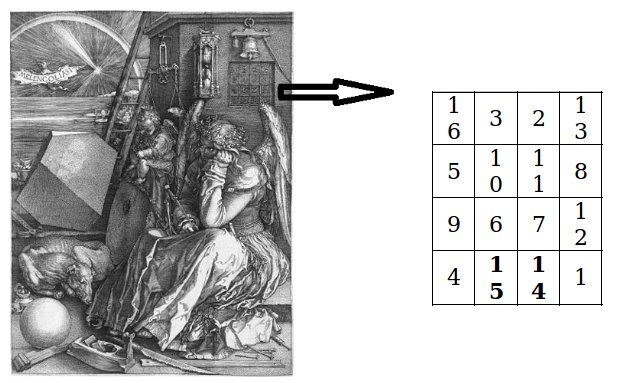
La construcción de cuadrados mágicos es un pasatiempo muy antiguo apareciendo ejemplos desde el año 2000 A.C. Los más habituales son los de 3×3 y 4×4. Aquí tenemos un ejemplo, aparece en el grabado Melancolía I de Alberto Durero de 1514.
Otro ejemplo de cuadrado mágico lo encontramos en la fachada de la Pasión, en la Sagrada Familia, aunque no es exactamente mágico ya que algunos números se repiten.
Tangram: Es un rompecabezas muy antiguo de origen chino. Consta de siete piezas y con ellas se pueden hacer muchas figuras. El objetivo es formar esas figuras cumpliendo un par de reglas muy sencillas
- Usar las siete piezas
- No superponer ninguna
 |
 |
Torres de Hanoi: Rompecabezas inventado en 1883 por el matemático Édouard Lucas. ¿Cuántos movimientos, como mínimo, se tendrán que realizar para pasar las fichas del soporte donde están a uno de los otros que está vacío? Las reglas son muy sencillas:
- Sólo se puede mover un disco cada vez.
- Un disco de mayor tamaño no puede estar sobre un disco más pequeño.

Existe también una leyenda del origen de este rompecabezas que cuenta que hace mucho tiempo, los monjes de un monasterio ubicado en la región de Hanói, Vietnam, se encontraban rezando a sus tres dioses: Brahma (el dios creador), Vishnu (el dios conservador) y Shiva (el dios destructor), ya que querían saber cuándo iba a ser destruido el mundo.
En respuesta a sus plegarias, se apareció ante ellos el dios Brahma y les entregó una base con tres postes, los cuales eran de diamante y del grosor del aguijón de un avispón, en uno de ellos se encontraban apilados 64 discos de oro puro de diferentes tamaños, siendo el disco más pequeño el que se encontraba en la punta de la torre, después un disco más grande, y, así sucesivamente, hasta llegar a la base de la torre donde se encontraba el disco de mayor tamaño. Una vez que el dios Brahma se retiró, los monjes se preguntaban qué debían hacer con los discos, en ese momento se manifestó el dios Vishnu y les explicó las reglas que describimos al inicio. Los monjes se alegraron de saber lo que tenían que hacer y pensaron que si movían todos los discos de un poste al otro cumpliendo las reglas que les había sido explicadas, complacerían a sus dioses y estos les dirían cuándo se terminaría el mundo. Cuando estaban a punto de comenzar a mover los discos, hizo su aparición el dios Shiva y les dijo: ‘’cuando terminen de mover los 64 discos, en ese momento el mundo habrá terminado’’. Los monjes se llenaron de miedo, pues si no movían los discos, sus dioses se enfadarían con ellos y los castigarían, pero si terminaban de mover todos los discos, entonces el mundo llegaría a su fin.
Para acabar: Usando ocho palillos realizar una figura formada por dos cuadrados y cuatro triángulos.
Esto no es más que una pequeña selección de la enorme cantidad de juegos existentes y que hoy en día tenemos disponibles en internet. No pretendo más que despertar un poco la curiosidad por ellos.
Desde luego no creo que el objetivo principal del docente sea hacer las clases divertidas pero estoy seguro que teniendo en cuenta este componente lúdico y creando un ambiente positivo conseguiremos captar el interés de los alumnos, el aprendizaje será más efectivo y más fácil alcanzar nuestro objetivo final: que aprendan Matemáticas.
Manuel Solivella Ortuño