T2: Técnicas de Conteo

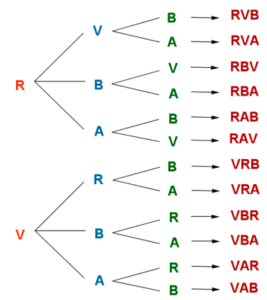
Disponemos de los colores rojo, verde, blanco y amarillo para formar todas las banderas posibles con tres franjas horizontales y la primera franja no queremos que sea blanca ni amarilla. Dibuja un diagrama de árbol que represente todas las banderas resultantes de manera que no se repitan colores en la misma bandera.

Si en un restaurante hay posibilidad de escoger 2 primeros, 2 segundos y 34 postres ¿cuántos menús diferentes se pueden hacer?
2 primeros · 2 segundos · 34 postres = 136 menús diferentes

¿Cuántos números telefónicos es posible diseñar considerando que dichos números deben constar de seis dígitos tomados del 0 al 9?
a) Si el 0 no puede ir al inicio y es posible repetir dígitos:
9 x 10 x 10 x 10 x 10 x 10 = 900.000 números telefónicos
b) Si el 0 no debe ir en primera posición y no es posible repetir dígitos
9 x 9 x 8 x 7 x 6 x 5 = 136.080 números telefónicos
c) ¿Cuántos de los números telefónicos del caso b empiezan por el 7?
1 x 9 x 8 x 7 x 6 x 5 = 15.120 números telefónicos

Si se desea llevar a efecto una actividad, la cual tiene formas alternativas para ser realizada, donde la primera de esas alternativas puede ser realizada de M maneras o formas, la segunda alternativa puede realizarse de N maneras o formas….. y la última de las alternativas puede ser realizada de W maneras o formas, entonces las opciones de realizarla
se calculan:
PA = [M + N +………+ W] maneras o formas

También se denomina de la Criba, y permite calcular el número
de elementos de la unión de varios conjuntos utilizando el cardinal de esos conjuntos y todas sus intersecciones.
Card(A U B) = Card(A) + Card(B) – Card(A intersección B)

Se sabe que en un grupo de trabajo de 33 personas, hay 15 personas que toman té, 27 que toman café. ¿Suman más de 33? Eso es porque hay personas que toman té y café, ¿cuántas?
Llamamos A a tomar el té, y B a tomar café. Entonces:
Card(A U B) = Card(A) + Card(B) – Card(A intersección B)
33 = 15 + 27 – Card(A intersección B)
Luego hay 9 personas que toman ambas bebidas.

Si metemos N +1 o más palomas, en N palomares entonces algún palomar debe contener dos o más palomas.

En un sobre tenemos tarjetas de dos colores, blancas y rojas, ¿cuál es el menor número de tarjetas que debemos sacar, para sin mirarlas, estar seguros de que al menos hay dos del mismo color?
La primera tarjeta podría tener uno de los dos colores, si la segunda repite color, ¡ya hemos ganado!, pero puede tener un color distinto. Pero al sacar la tercera, ya es seguro que tiene que tener el color de alguna de las que ya hemos sacado. Sacar dos tarjetas no es suficiente. Pero con tres, es seguro que hay dos con el mismo color.
Vamos a verlo ahora usando el Principio del Palomar. Las tarjetas desempeñan el papel de las palomas. Y los dos colores, el de los palomares. 3 palomas no pueden estar en 2 palomares, luego se repite color.