Inicio > 4ºESO B > Ampliación 4ºESO > T2: Polinomios y fracciones algebraicas

T2: Polinomios y fracciones algebraicas

4ºESO B

21 de agosto de 2024

RECUERDA LA SUMA, RESTA Y PRODUCTO DE POLINOMIOS

SUMA, RESTA Y PRODUCTO DE POLINOMIOS
– p62 Ej 1 (solución) p62 Ej 1 (paso a paso)
– p75 Ej 1
– p75 Ej 2
– p75 Ej 8

IDENTIDADES NOTABLES
– p75 Ej 3
– p75 Ej 4
– p75 Ej 6
– p75 Ej 5
– 2 ejemplos más tipo el ejercicio 5
– p75 Ej 7

FICHAS DE IDENTIDADES NOTABLES

– Ficha 0 muy sencilla con las soluciones
– Ficha 1 identidades notables (también sencilla, de desarrollar y con soluciones)
– Ficha 2 más completa (con soluciones)
– Ficha 3 identidades notables (más complicada, con soluciones)

REPASO DE DIVISIÓN DE POLINOMIOS

EJEMPLO DE DIVISIÓN DE POLINOMIOS:

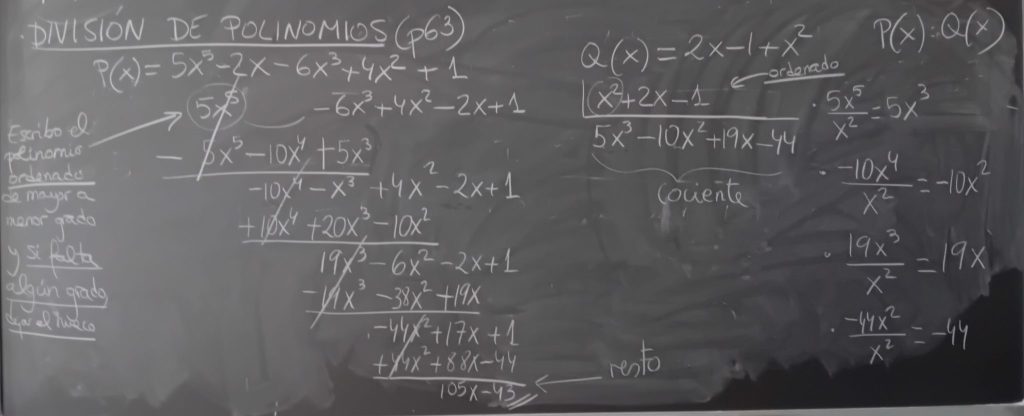
EXPRESAR EL DIVIDENDO EN FUNCIÓN DE LA DIVISIÓN:

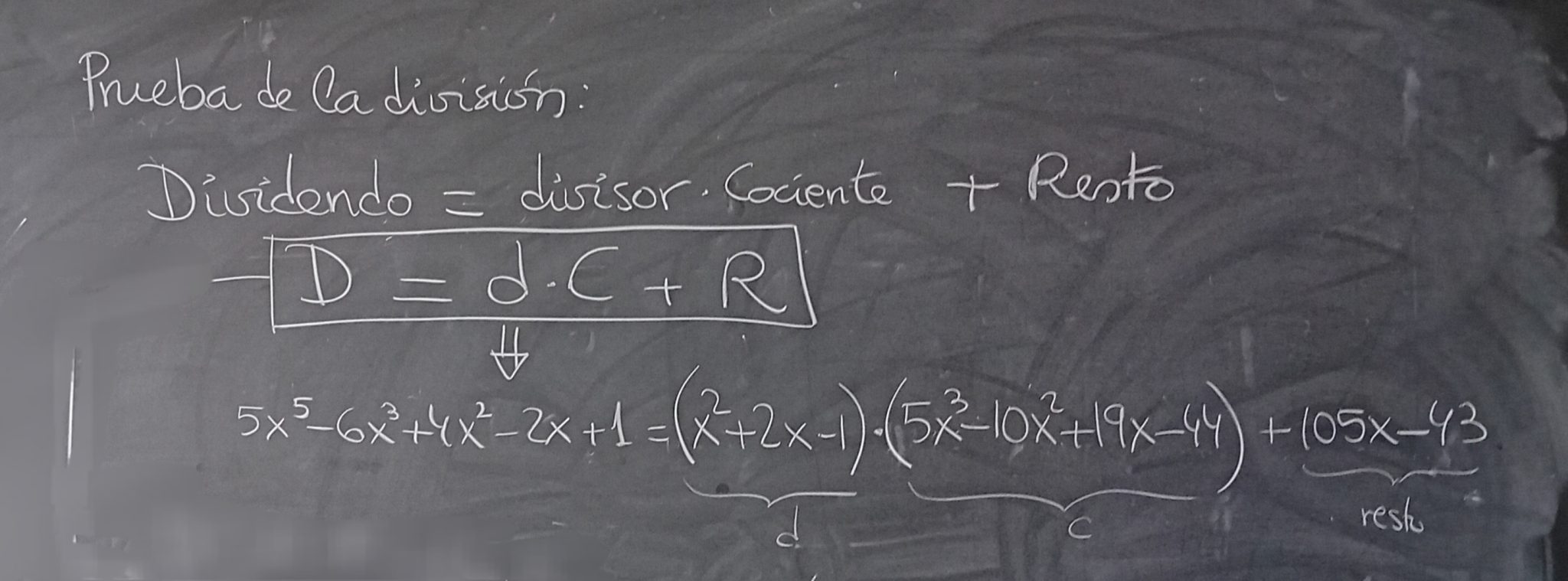
EXPRESAR A QUÉ ES IGUAL LA DIVISIÓN:

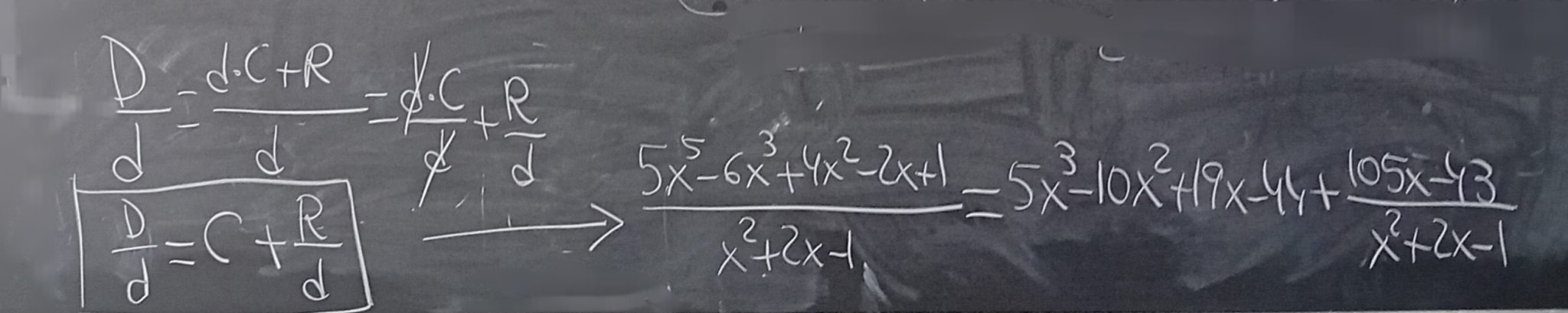
– p75 Ej 9 (Resuelto en la pizarra a, b y c )
– p75 Ej 10 (Resuelto en la pizarra a )
.

RUFFINI

Ejemplos del método de Ruffini (del libro de Santillana antiguo).

CONCEPTO DE RAÍZ DE UN POLINOMIO Y TEOREMA DEL RESTO

Ejercicios:

p65:	Ej 4
p76:	Ej 31	Ej 32
p77:	Ej 42 y 43	Ej 45 y 46	Ej 47	Ej 48 y 49
p78:	Ej 50

FACTORIZACIÓN DE POLINOMIOS

PASOS PARA FACTORIZAR UN POLINOMIO

1º.- Si se puede, sacar factor común.

2º.- Sobre el polinomio que ya no tiene ningún factor común, si es de grado mayor que 2, factorizar buscando raíces enteras por Ruffini.

Si no encontramos ninguna raíz entera, no podremos factorizarlo.
Si encontramos algunas raíces enteras pero no llegamos con Ruffini hasta un cociente de grado 1 ó 0:
- si el cociente es de grado 2, pasar al paso 3.
- si el cociente todavía es de grado mayor que 2, factorizaremos con las raíces que hayamos sacado y nos quedará un factor de grado mayor que 2 que no podremos factorizar más.

3º.- Si el polinomio es de grado 2, factorizar aplicando:

Identidad notable si lo es.
(También se podría encontrar una identidad notable con un grado mayor en cualquier momento. Si la identificamos, sea del grado que sea, pasarla a factores siempre nos ayudará a la factorización, aunque no estemos en este paso de polinomio de grado 2).
Buscar las raíces mediante la ecuación de segundo grado (recordar no olvidar el coeficiente del término x² ).
Buscar las raíces mediante Ruffini

4º.- Si el polinomio es de grado 1, ya no se puede factorizar más, salvo que podamos sacar factor común algún número (sin x).

EJEMPLO:

Otro ejemplo de factorización de polinomio completo
.

Ejercicios de Factorización de Polinomios (Anaya)

p69:	Ej 1	a	b	c	d	e	f
p76:	Ej 29	a y b	c y d	e y f
p76:	Ej 30	a y b	c y d	e y f
p76:	Ej 31	Ej 32
p78:	Ej 54

DIAGRAMA DE FLUJO

Un diagrama de flujo es una representación gráfica (y por lo tanto muy visual) de una tarea que se puede descomponer en una secuencia lógica de pasos ordenados.

Lo primero que hemos de hacer es definir la tarea que queremos representar mediante el Diagrama de Flujos. Una vez tenemos clara la tarea, debemos hacer una descripción secuencial de los pasos que tenemos que seguir para cumplir el objetivo. Preferentemente por escrito.

Por ejemplo, Imaginemos que hemos ido al supermercado y queremos pagar con nuestra tarjeta de crédito contactless. La secuencia que seguimos es la siguiente:

Acercamos la tarjeta al terminal.
Una vez en la pantalla de PIN, introducimos nuestro pin.
Si el pin es correcto, el pago se efectúa.
Si el pin no es correcto, lo volvemos a introducir.
Si ponemos tres veces mal el pin, el terminal no aceptará la transacción.

Una vez tenemos los pasos descritos, podemos hacer la representación gráfica de estos en el siguiente flujo (se muestran también los elementos más utilizados:

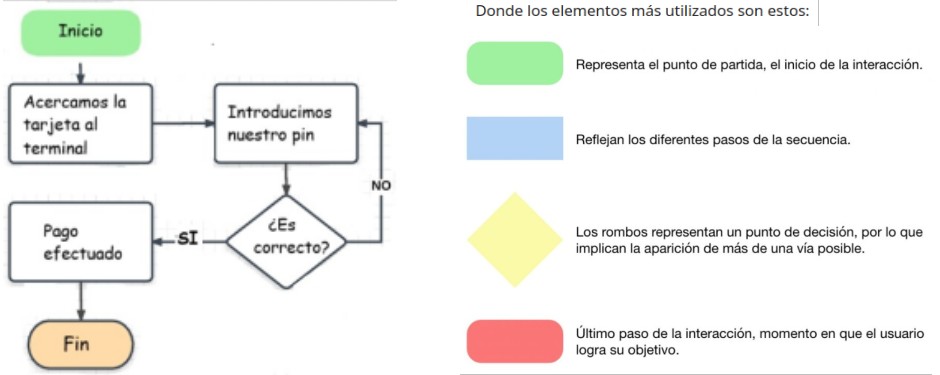
¿Serías capaz de hacer un diagrama de flujo que refleje los pasos a seguir para factorizar un polinomio?
Posible Solución

FRACCIONES ALGREBRAICAS

(+ , -) PASOS PARA SUMAR/RESTAR FRACCIONES ALGEBRAICAS

1º.- Factorizar todos los denominadores.

2º.- Sacar el mínimo común múltiplo de todos los denominadores ya factorizados (factores comunes al mayor exponente y factores no comunes). Ese es el denominador común.

3º.- Poner el denominador común en cada fracción y multiplicar en cada numerador por los factores correspondientes (como se hace cuando son fracciones numéricas).

4º.- Sumar/restar los numeradores, manteniendo el denominador común que hemos calculado al principio. Es probable que en este paso, en el numerador común haya que hacer varias multiplicaciones y reducir al final el polinomio del numerador.

5º.- No hemos multiplicado en ningún momento el denominador, lo hemos mantenido en factores.

6º.- Comprobar si se pueden simplificar el numerador y el denominador. Para ello podemos hacer 2 cosas:

Comprobar si alguna de las raíces del denominador es también raíz del numerador. Si es así, hay que factorizar el numerador, pues hay algún factor común. Si ninguna raíz es común, no podremos simplificar más.

Factorizar el numerador y si hay factores comunes, simplificarlos. Esta forma es más larga que la anterior y en muchas ocasiones no conseguiremos factores comunes.

7º.- Una vez está simplificado al máximo, operar el numerador y el denominador para que queden en forma de polinomios (no en factores).

( x , / ) PASOS PARA MULTIPLICAR/DIVIDIR FRACCIONES ALGEBRAICAS

1º.- Si es una división, multiplicar los términos en cruz, sin hacer la operación, dejándola indicada, de forma que en el numerador tengamos la multiplicación de varios polinomios y en el denominador lo mismo. Ahora ya es como si tuviéramos una multiplicación.

2º.- IMPORTANTÍSIMO no hacer ninguna multiplicación, dejarlas todas indicadas.

3º.- Factorizar todos los polinomios que tengamos, mediante alguna de las formas de factorización de polinomios que conocemos.

4º.- Simplificar los factores que aparezcan en numerador y en denominador a la vez.

5º.- Cuando ya no queden factores comunes entre el numerador y el denominador, no se podrá simplificar más.

6º.- Multiplicar los factores que hayan quedado para dejar el resultado como una fracción algebraica con un polinomio en el numerador y otro en el denominador.