
TRISECTRIZ DE UN ÁNGULO
Como os comenté en la entrada anterior vamos a ver como dividir un ángulo en 3 partes iguales utilizando la espiral de Arquímedes.
En primer lugar debemos dibujar la espiral de Arquímedes sobre unos ejes cartesianos. A continuación, colocaríamos el vértice del ángulo que queremos trisectar sobre el origen de la espiral y uno de los lados del ángulo sobre el semieje positivo de las abcisas.
Una vez tenemos situado el ángulo donde corresponde, comprobaremos que el otro lado del ángulo es cortado por la espiral en un punto al que llamaremos Q. Ahora, debemos dividir el segmento OQ en 3 partes iguales (usando el teorema de Tales o bien una regla graduada).Llamaremos a los puntos intermedios Q1 y Q2.
Por último, con la ayuda de un compás, haciendo centro en O, trazaremos arcos de circunferencia por los puntos Q1 y Q2, los cuales cortaran a la espiral en otros 2 puntos a los que llamaremos H1 y H2; y uniremos estos puntos con O obteniendo las dos semirrectas que dividen al segmento en 3 partes iguales.
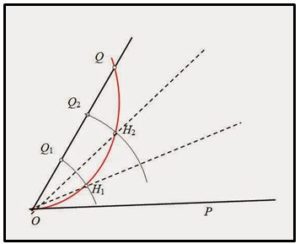
Este mismo método se puede generalizar para dividir un ángulo en n partes iguales.
Ponlo a prueba!!!


 Anterior
Anterior 

