TEOREMA DE PICK. Cálculo de áreas

Si en una hoja cuadriculada dibujamos un polígono simple, colocando sus vértices en los puntos donde se cortan los cuadritos, hay un método muy sencillo que nos permite calcular su área. Este cálculo se realiza utilizando el teorema de Pick.

Este teorema nos da una fórmula para su cálculo.

Veamos que dice el teorema:

«Sea un polígono simple cuyos vértices tienen coordenadas enteras. Si B es el número de puntos enteros en el borde, I el número de puntos enteros en el interior del polígono, entonces el área A del polígono se puede calcular con la fórmula: A=  I + B/2 – 1»

Hemos hablado de los polígonos simples, pero ¿Cuáles son? 

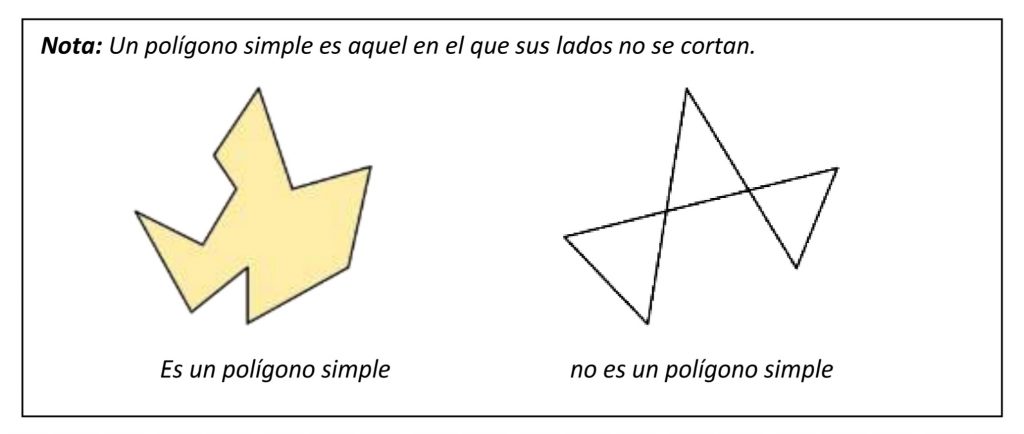
A continuación, calcularemos el área de tres polígonos muy conocidos de los que todos conocemos la fórmula que nos permite calcular su área y podríamos comprobar que el resultado que se obtiene con el teorema de Pick es el mismo.

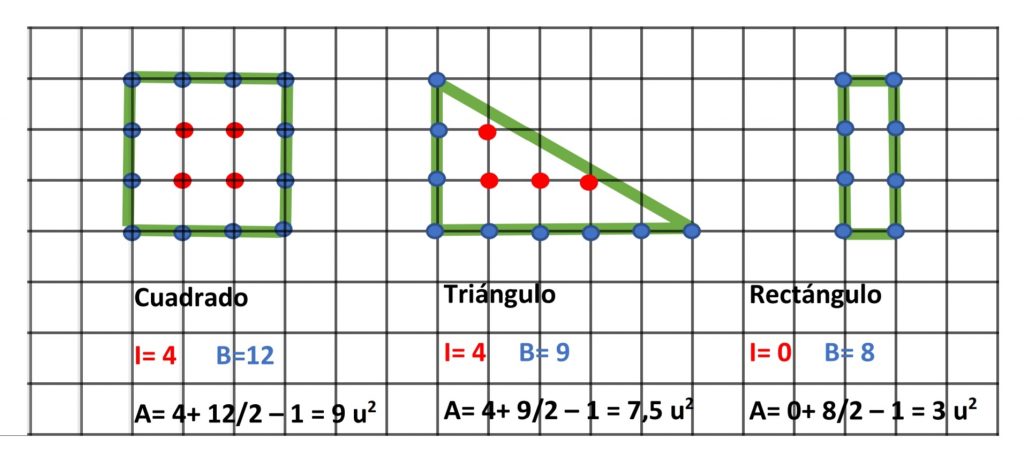
Para acabar, te propongo que calcules el área de los siguientes polígonos simples utilizando el teorema de Pick:

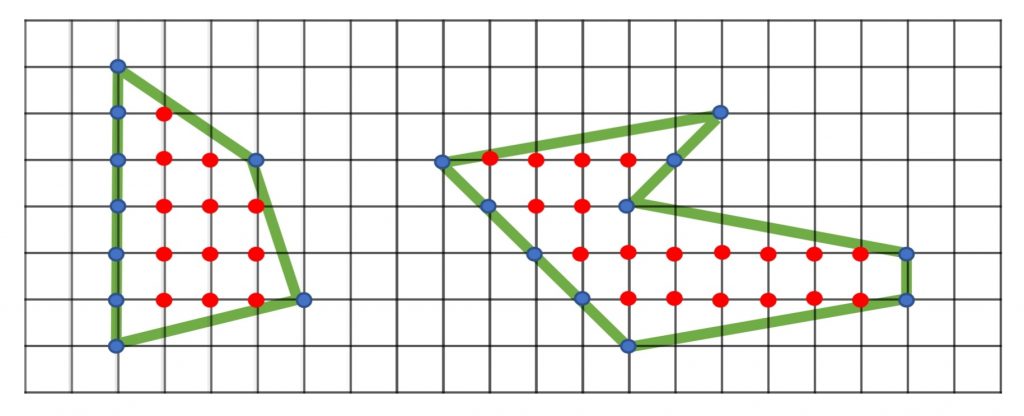
Puedes descargarte la ficha de esta entrada pinchando aquí. En ella encontrarás la solución del ejercicio propuesto.

Además, te invito a que averigües algo más sobre el matemático austríaco Georg Alexander Pick, quien en 1899 describió el resultado de este teorema.