SUCESIONES RECURRENTES: SUCESIÓN DE SYLVESTER

Sabemos que una manera de definir una sucesión, además de por su término general, es por recurrencia.

Las sucesiones recurrentes son aquellas cuyos términos, después de dados uno o varios consecutivos, se obtienen a partir de los anteriores.

La más conocida es la sucesión de Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21, 34…

Los términos de la sucesión de Fibonacci se obtiene sumando los dos anteriores, sabiendo que a₁ =1 y a₂ = 1. Ley de recurrencia:

Si quieres saber más sobre la sucesión de Fibonacci, visita la entrada: Propiedades de la sucesión de Fibonacci

Pero no es la única, también os hable de la sucesión de Pell en la entrada: Número de Plata

La sucesión de Pell se define de manera similar a la de Fibonacci, si a₁ =0 y a₂ = 1, los demás términos se obtienen sumando el doble del anterior más el anterior a éste. Algunos términos de esta sucesión son: 0, 1, 2, 5, 12, 29, 70… Ley de recurrencia:

Otra sucesión recurrente es la sucesión de Padovan, se define igual que la de Fibonacci, se consideran a₁ =1, a₂ =1 y a₃ =1 y los términos de la sucesión se obtienen sumando los dos términos anteriores al anterior que queremos calcular. La sucesión sería: 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16… Ley de recurrencia:

Antes de hablar de la sucesión de Sylvester, vamos a ver otras dos:

• Sucesión de Lucas. Si a₁ =2 y a₂ =1, los demás términos se obtienen sumando los dos anteriores, al igual que en la sucesión de Fibonacci, y tenemos que la sucesión es: 2, 1, 3, 4, 7, 11… Ley de recurrencia:
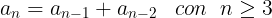
• Sucesión de Perrin. Si a₁ =3, a₂ =0 y a₃ =2 los demás términos se obtienen sumando el anterior y el anterior del anterior a éste, y tenemos la sucesión: 3, 0, 2, 5, 5, 7, 12, 17, 24… Ley de recurrencia:

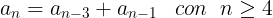
Como habrás observado, los términos de las sucesiones anteriores se obtienen sumando términos anteriores. La diferencia de la sucesión de Sylvester con éstas es que se obtienen multiplicando. Pasemos a definirla.

La sucesión de Sylvester es una sucesión de números enteros de los que conocemos a₁ =2 y a₂ = 3 y en la que cada término es el producto de todos los anteriores, más uno. Algunos de sus términos serían: 2, 3, 7, 43, 1807, 3263443, 10650056950807… Ley de recurrencia: . También se puede expresar como

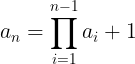
Vemos que los término crecen muy rápidamente. El motivo de hablaros de esta sucesión es porque tiene relación con las entradas anteriores en las que hablábamos de las fracciones egipcias; y es que la suma de sus inversos es una serie de fracciones unitarias que converge a 1.

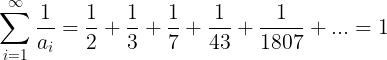
Pero, para acabar, lo que me gustaría destacar, es que podemos encontrar representaciones finitas en forma de fracción egipcia de la unidad, de cualquier longitud, truncando esta serie y restando uno del último denominador.

Veamos algunos ejemplos:

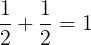
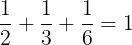
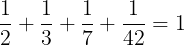
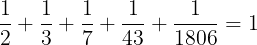
Qué interesante!!!!