Proporciones áurea y cordobesa
A Euclides, se le conoce como el padre de la geometría. Su obra más famosa sin duda es “Elementos” en la que compiló los conocimientos matemáticos de su época.
En él, hay un extenso estudio sobre las proporciones. En esta entrada os voy a nombrar dos de ellas que se obtienen a partir de relacionar el lado del polígono con el radio de la circunferencia en la que se inscribe.
Estos polígonos son el decágono regular y el octógono regular.
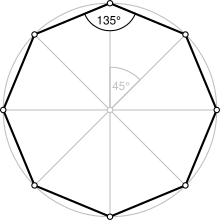
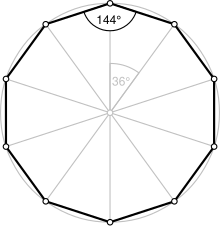
Llamamos L a la longitud del lado y R al radio de la circunferencia.
Calculemos R/L en ambos casos. Para calcular L aplicaremos el teorema del coseno en uno de los triángulos isósceles en los que queda dividido el polígono.
OCTÓGONO
L2=R2+R2-2·R·R·cos 45º
L2= 2R2-2R2·
/2
L2=2R2(1-/2)=R2(2-)
L =R·
Luego
DECÁGONO
En primer lugar, debemos saber que cos36º=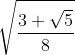
L2=R2+R2-2·R·R·cos 36º
L2= 2R2-2R2·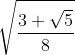
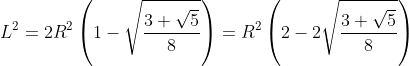
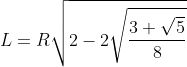
Luego
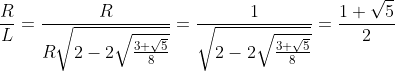
Estos dos números que hemos obtenido, 
y 
, son dos proporciones muy conocidas.
La primera de ella, desde hace medio siglo recibe el nombre de proporción cordobesa, denominación que le dio el arquitecto Rafael de la Hoz Arderius tras realizar un estudio en la ciudad de Córdoba. La segunda, seguramente os sonará más, ya que es la proporción áurea.
Si en vez de basarnos en la geometría, lo hubiéramos hecho en el álgebra. Estas proporciones son la solución de dos ecuaciones:
La proporción cordobesa se obtiene al resolver la ecuación: 2X4-4X2+1=0, mientras que la proporción áurea al resolver la ecuación X2-X-1=0.
Os invito a que busquéis más información sobre estas dos proporciones.
AMPLIACIÓN:
- ¿Cómo se construye el rectángulo de oro? ¿Y el rectángulo cordobés?
- Con el decágono regular, hemos obtenido el número de oro. ¿Con qué polígono se obtiene el número de plata? ¿Cómo se obtiene la razón plateada? ¿De qué ecuación es solución el número plateado?
Anterior 
