La solución matemática a un problema irresoluble

Enunciado: Coje una tira de papel, dibuja en ella 3 cuadrados que esten alineados y en frente de cada uno de ellos 3 círculos. Intenta unir cada uno de los cuadrados con los tres círculos que tienen enfrente sin que las lineas se corten.

Inténtalo hacer antes de continuar leyendo.

Después de varios intentos habrás comprobado que es imposible resolverlo.

Existe en matemáticas una teoria que demuestra que este problema no tiene solución, la teoría de grafos.

Curiosidad: La teoría de grafos se originó tras la resolución por parte de Leonard Euler del problema de los puentes de Königsberg en 1936.

En la entrada anterior, os hablaba de figuras imposibles y de las litografías de Escher.

Una de las litografías del universo matemático de este artista es cinta de moebius II (1963) en la que una serie de hormigas recorren una cinta sin fin.

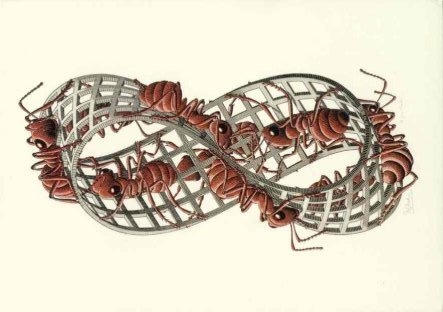
Pero ¿qué es la cinta de möebius y como se construye?

La cinta de moebius  es una superficie con una sola cara y un solo borde. Tiene la propiedad matemática de ser un objeto no orientable. También es una superficie reglada. Fue descubierta de forma independiente por los matemáticos alemanes August Ferdinand Möbius y Johann Benedict Listing en 1858.

Para construirla, se toma una tira de papel y se pegan los extremos dando media vuelta a uno de ellos antes de pegarlos.

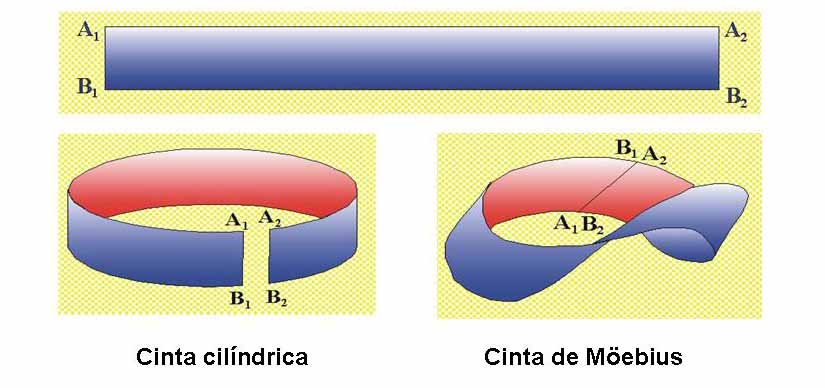
Curiosidades: 

Al cortar longitudinalmente la cinta de möebius se obtienen resultados curiosos según por donde se realize el corte. (busca información en la red)

La cinta de möebius ha sido utilizada en arquitectura, pintura, escultura, mecánica, ingenieria, moda, diseño, joyería, cine, música, literatura…

Además, el símbolo del reciclaje creado por Gary Anderson en 1970 es una cinta de möebius  y representa el proceso de transformación del material de deshecho en recursos útiles. La regla de las 3 R (Reduce – Reutiliza – Recicla)

Recuerda que una de las líneas de actuación de nuestro PEC trata sobre el reciclaje.

Solución: Ahora si que estamos en condiciones de resolver el problema, pues basta en transformar la tira de papel en la que habíamos dibujado los cuadrados y los círculos en una cinta de moebius, y de esta forma al tener la cinta una sola cara podemos unirlos sin que las líneas se corten.

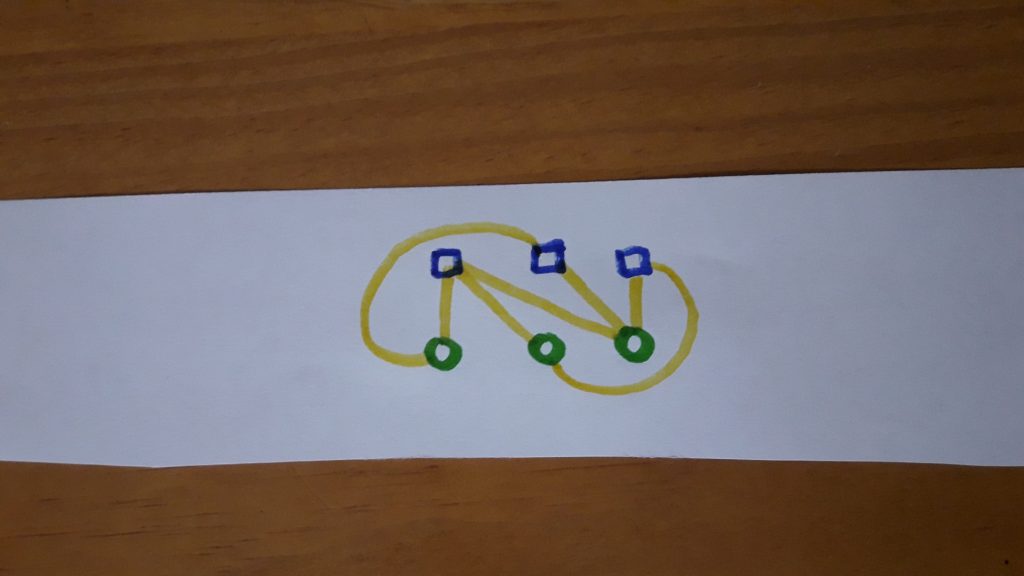
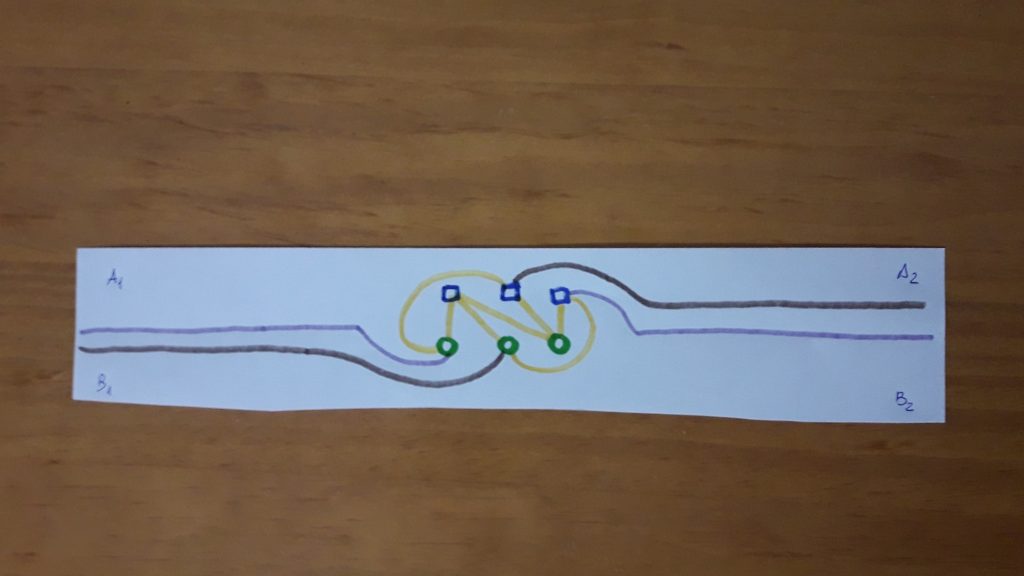
Curioso, ¿verdad?