FRACCIONES CONTINUAS

Definición

Las fracciones continuas son expresiones de la forma:

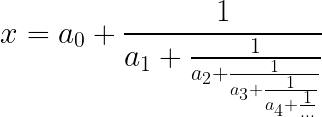
donde a₀ es un número entero y los demás a_i son enteros positivos. Los números a₀, a₁ ,a₂ ,a₃ … se llaman cocientes incompletos.

Nota: en el caso de que los numeradores puedan tomar valores diferentes de 1, se dice que es una fracción continua generalizada.

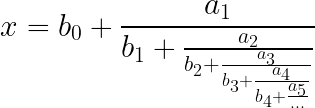
Para distinguir la primera de la generalizada, se le llama también fracción continua regular o simple.

El motivo de introducir este concepto es porque Euler demostró que todo número racional puede expresarse mediante una fracción continua finita y que todo número irracional puede expresarse mediante una fracción continua infinita.

Ejemplo

A continuación, vamos a ver como expresar un número racional como una fracción continua.

Consideramos el número

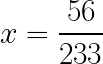
Para obtener los diferentes cocientes incompletos debemos utilizar el algoritmo de Euclides que nos dice que , es decir,

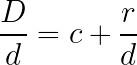
Al realizar la división obtenemos que el cociente es 0 y el resto 56, luego tenemos que

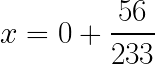
El primer sumando será siempre 0 si la fracción propia, es decir, que el numerador es menor que el denominador.

Después de realizar cada división deberemos usar la propiedad

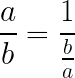
De modo que nos queda:

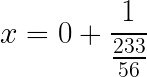
Repetimos el proceso hasta obtener la fracción continua como sigue:

Dividimos 233 entre 56, el cociente da 4 y el resto 9,

Invertimos la fracción resultante

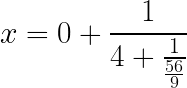
Dividimos 56 entre 9, el cociente da 6 y el resto 2

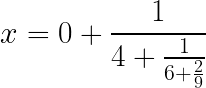
Volvemos a invertir la fracción resultante

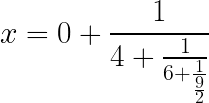
Dividimos 9 entre 2, el cociente da 4 y el resto da 1 y se finaliza el proceso. La fracción continua resultante es:

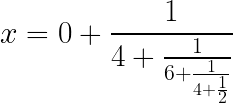
Irracionalidad de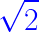

En otra entrada, vimos que era irracional demostrándolo por reducción al absurdo. Ahora vamos a expresarla como una fracción continua infinita:

Para demostrarlo vamos a partir de la siguiente identidad notable:

Despejamos

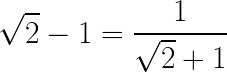
Sumamos 2 unidades a cada lado de la igualdad

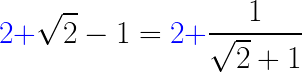
Simplificamos

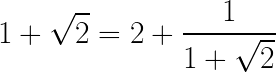
Observamos que el denominador podemos sustituirlo por la expresión que acabamos de obtener y quedaría

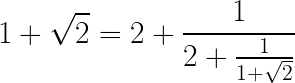
Este proceso se puede repetir indefinidamente:

Si seguimos obtendríamos que

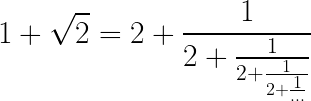
Despejando tenemos que

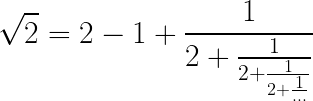
Luego la fracción continua de es:

La cual es infinita y por tanto es irracional

Irracionalidad de  π

Gracias a Euler, Lambert, coetáneo con él, demostró que el número  π  era irracional. Lo hizo usando la fracción continua de la tangente (tan α), teniendo en cuenta que tan( π/4) =1.

Existe otra demostración por reducción al absurdo de Ivan Niven de la irracionalidad de  π. Podéis ver como lo explica Eduardo Sáenz en su canal de YouTube «derivando» en el siguiente enlace: Irracionalidad de  π

Calculadora de fracciones continuas

A continuación, os dejo un calculadora que he encontrado en la web www.epsilones.com, en la que podéis obtener la fracción continua de cualquier número racional e irracional. En el caso de éstos últimos, veréis que la fracción continua es infinita. Podéis probarlo con los números irracionales que ya conocemos como las raíces cuadradas de 2, de 5, el número  π, el número e, el número áureo

También podéis calcular la fracción continua de algunos números racionales y comprobad si lo habéis hecho bien con la calculadora. Os animáis!!!