
Día internacional de la matemáticas 2025
El 14 de marzo se celebra desde hace unos años el día internacional de las matemáticas.
Este año el tema del IDM celebra la creatividad que se encuentra en el descubrimiento matemático y el arte.
Os dejo el enlace: Temática IDM314
En esta ocasión os quiero hablar del símbolo del infinito, el cual ha servido de inspiración a artistas para elaborar sus creaciones, basta sumergirse en in Internet y encontrar cuadros, esculturas…
El símbolo del infinito, es una curva que en matemáticas recibe el nombre de lemniscata.
En esta entrada, quiero que conozcáis su definición y como se obtiene su ecuación matemática.
En particular estudiaremos la lemniscata de Bernoulli.
Se define como: «lugar geométrico de puntos P, tales que el producto de su distancia a los focos es constante y vale d2, siendo d la semidistancia focal.«
d(P, F)·d(P, F’)=d2
A continuación, obtendremos su ecuación reducida, es decir, aquella que está centrada en el origen de coordenadas.
Los focos los consideraremos sobre el eje de abcisas.
La ecuación la obtendremos para el caso particular en el que d=1, es decir, los focos se encuentran en los puntos F(1, 0) y F’(-1, 0).
Empecemos:
Consideramos un punto cualquiera de la lemniscata P(x,y). Sabiendo que la distancia entre dos puntos es el módulo del vector que forman, se obtiene que:
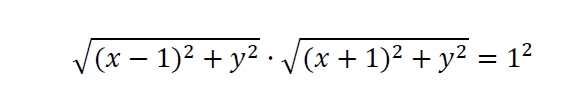
Elevamos al cuadrado los dos miembros de la igualdad:
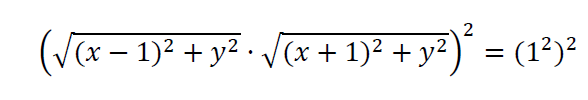
Desarrollamos la expresión:
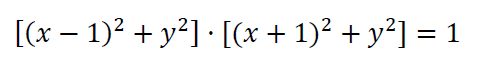
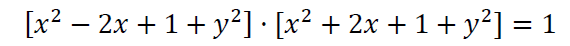
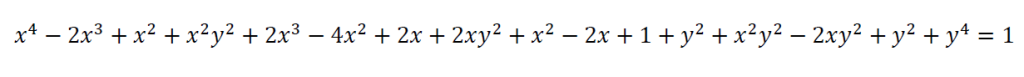
Simplificamos la expresión:
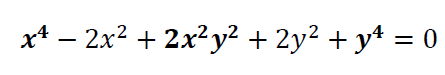
Usamos la identidad notable:
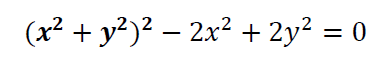
Sacamos factor común:
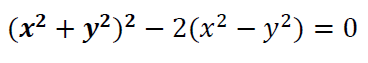
Su gráfica, haciendo uso de GeoGebra resulta:
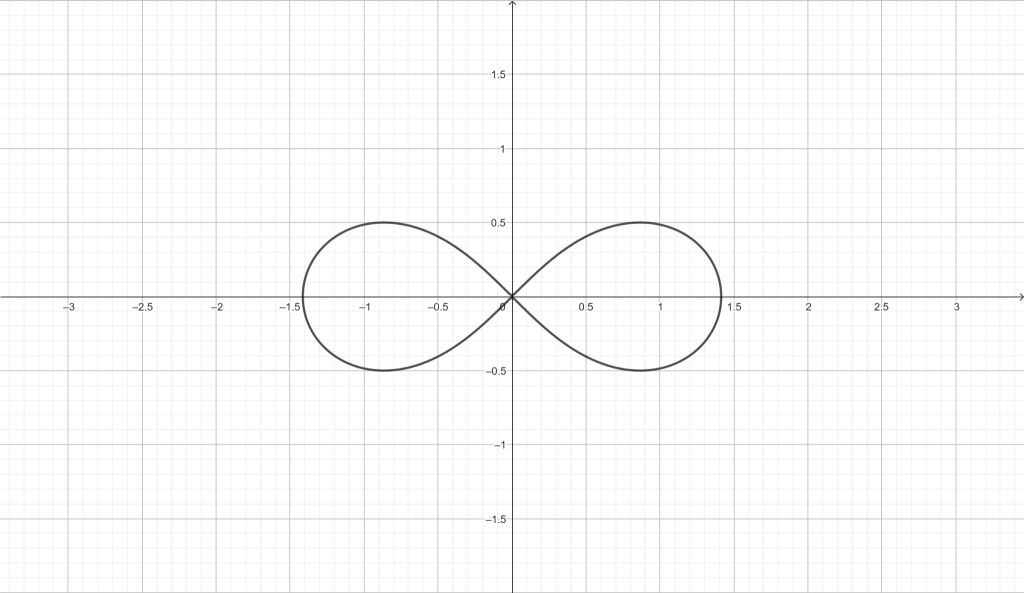
Y ahora te toca a tí:
Obtén la ecuación de la lemniscata de Bernoulli en función de d.
¿Te animas?


 Anterior
Anterior 

