
Corazón matemático
Este año, en 1º de bachillerato, acabamos de ver las cónicas y actualmente estamos estudiando las funciones elementales. Apliquemoslo en la siguiente entrada.
Vamos a analizar la gráfica de cada uno de los cuadrantes en que queda dividido el plano por los ejes coordinados y que forma este corazón matemático.
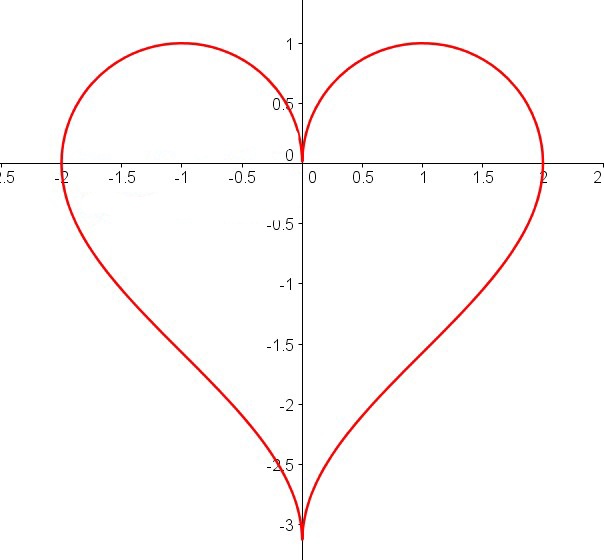
Ya que este corazón no corresponde a ninguna función. Podéis ver no cumple la definición ya que para cada valor de x, no existe un único valor de y.
Deduzcamos las 4 funciones que lo forman.
En los dos primeros cuadrantes tenemos 2 semicircunferencias, mientras que en el 3r y 4º cuadrante tenemos una curva sinusoidal que corresponde a una función arco. Encontramos la función de cada uno de los cuadrantes.
CUADRANTE I:
La semicircunferencia que hay representada corresponde a la circunferencia de centro C(1,0) y radio 1 y cuya ordenada es positiva.
Sabemos que la ecuación de una circunferencia de centro (a,b) y radio r viene dada por (x-a) 2 +(y-b) 2 =r 2
En nuestro caso sería: (x-1) 2 +(y-0) 2 =12
Si despejamos y tendriamos que

Como la ordenada tiene que ser positiva, la función sería

CUADRANTE II:
Del mismo modo, tendríamos esta semicircunferencia. Corresponde a la circunferencia de centro C(-1,0) y radio 1
La ecuación vendría dada por: (x+1) 2 +(y-0) 2 =1 2
Si despejamos tendríamos que:

Como la ordenada tiene que ser positiva, la función sería:

CUADRANTE III:
Recordemos como es la gráfica de la función arcocoseno:

Para obtener la grafica del tercer cuadrante vemos que debemos trasladar la gráfica 1 unidad a la izquierda y π unidades hacía abajo.
Para desplazarla 1 unidad hacia la izquierda debemos de cambiar x por x+1 y para desplazarla π unidades hacía abajo debemos restarle a la función π unidades.
De modo que la función que esta representada en el 3r cuadrante sería: y= arccos(x+1) – π
CUADRANTE IV:
Y para el cuarto cuadrante, basta con hacer una simetría respecto al eje X de la gráfica del 3r cuadrante.
De modo que la función sería: y= – [arccos(x+1) – π]


 Anterior
Anterior 

