CATENARIAS

Antes de definir “catenaria” voy a definiros las funciones hiperbólicas y alguna de sus propiedades.

Las funciones hiperbólicas se basan en la fusión exponencial y son análogas a las funciones trigonométricas, pero definidas usando la hipérbola en vez del círculo.

Definamos las funciones seno y coseno hiperbólicos. El resto de las funciones se obtienen de ellas dos.

Seno hiperbólico: se denota como senh(x) y se define como:

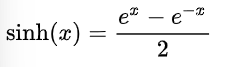
Coseno hiperbólico: se denota como cosh(x) y se define como:

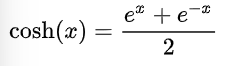
A partir de ellas dos definimos, al igual que en trigonometría, la tangente hiperbólica.

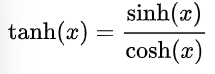
Y del mismo modo la secante, la cosecante y la cotangente hiperbólicas.

La propiedad fundamental que cumplen es:

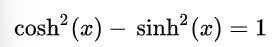
También es fácil comprobar que:

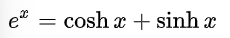
Podríamos seguir hablando de estas funciones, pero ahora que sabemos como se definen, veamos el concepto de catenaria.

En matemáticas y arquitectura se emplea la palabra catenaria para designar la curva cuyo trazado sigue la forma que adquiere una cadena o cuerda de densidad uniforme y perfectamente flexible sujeta por sus dos extremos y que se encuentra sometida únicamente a las fuerzas de la gravedad.

De todas las posibles catenarias, os voy a dar la función cuya gráfica corresponde a la curva formada por una cadena suspendida de dos puntos que se encuentran a la misma altura y cuyo mínimo se encuentra en el punto (0, a).

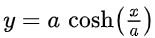
Siendo a una constate que se obtiene del cociente entre la componente horizontal que aparecerá entre los extremos y el peso por unidad de longitud de la cadena.

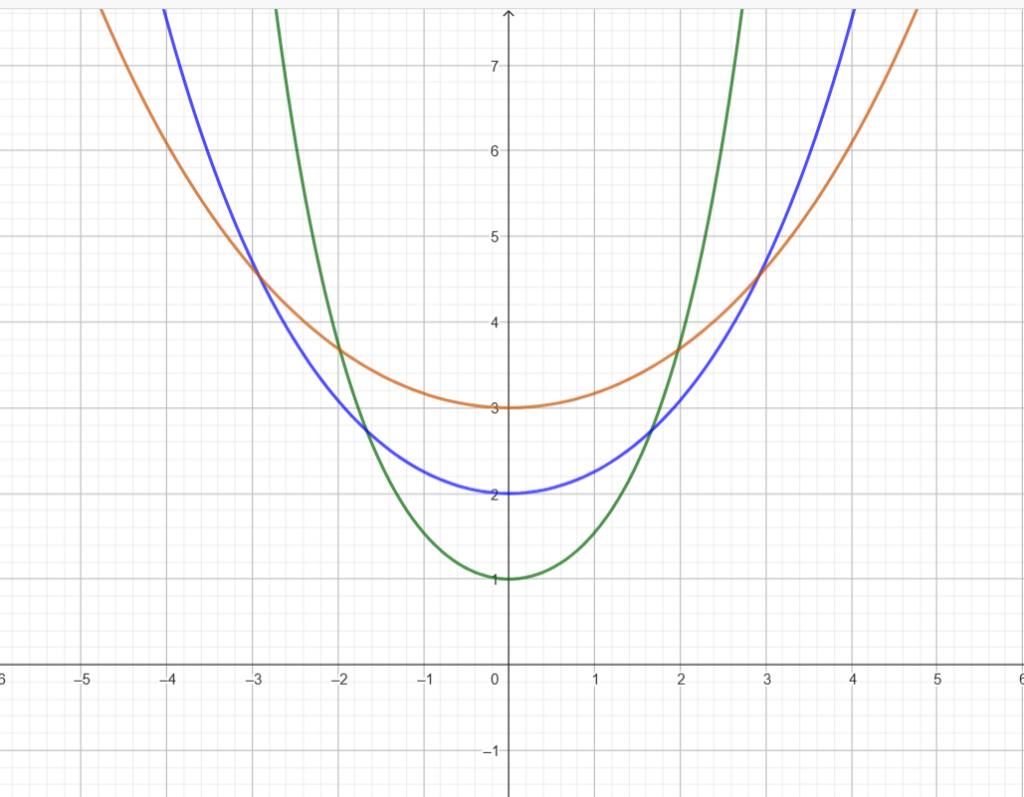
Veamos su gráfica dependiendo de los valores de a: Hemos tomado los valores 1, 2 y 3

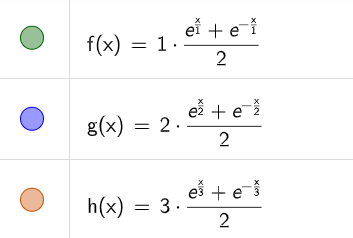
La longitud de esta cadena se obtendría con la fórmula:

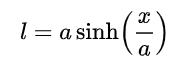
ACTIVIDAD:

El próximo día 25 de marzo, haremos la ruta matemática 1 por Valencia, y una de las paradas es en las Torres de Quart.

Si suponemos que el eje x está representado por el suelo y el mínimo de la catenaria esta situado sobre el eje y:

a) Calcula:

• la distancia del mínimo de la catenaria al suelo para obtener el valor de a.
• la distancia entre los dos postes donde se sujeta la cadena.
• la altura del suelo se sujeta la cadena en ambos postes
• la longitud de la cadena.

b) Representa con ayuda de GeoGebra la gráfica.