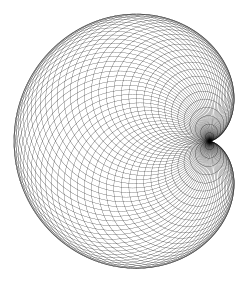
CARDIOIDE

En primer lugar vamos a recordar la relación entre las coordenadas cartesianas I(o rectangulares) y las coordenadas polares que vimos en el tema de números complejos.

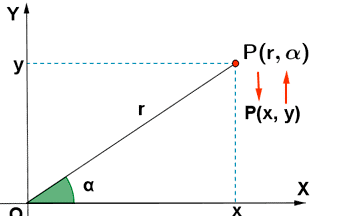
Para pasar de polares a cartesianas:

x = r·cosα

y = r. senα

Para pasar de cartesianas a polares:

​​​​​​​r ² =x ² +y ²

​​​​​​​tanα= y/x

​​​​​​​Sabiendo esto, veamos que es un CARDIOIDE :

​​​​​​​Un cardioide es la trayectoria que genera un punto de una circunferencia al girar sobre otra circunferencia.

​​​​​​​Vemos una animación:

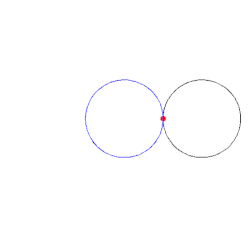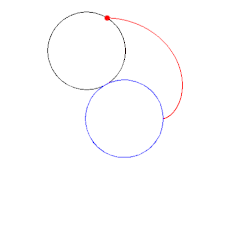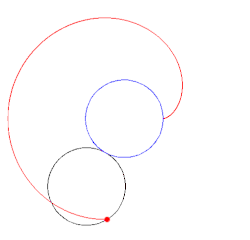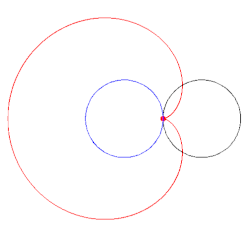
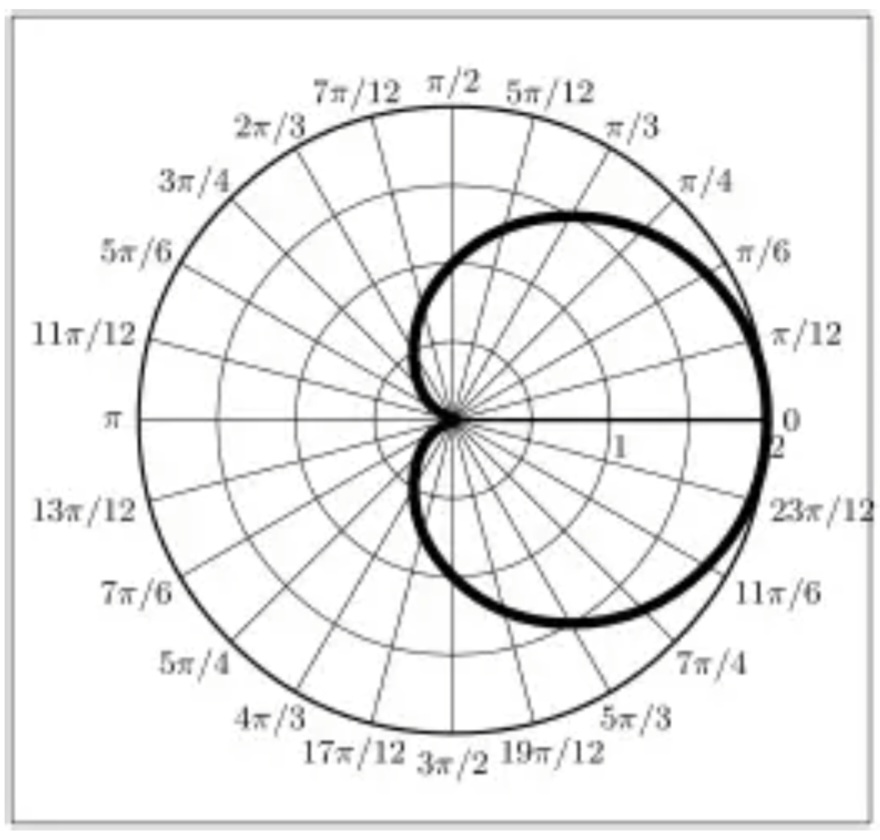
Su ecuación en coordenadas polares es: r= a(1+cosα) siendo a constante.

​​​​​​​Usando las ecuaciones de conversión, podemos obtener la ecuación en coordenadas cartesianas.

​​​​​​​Ecuación en coordenadas cartesianas: (x ² +y ² -2ax) ² =4a ² (x ² +y ²)

Representación:

Actividades :

​​​​​​​1. Transforma la ecuación en coordenadas polares a coordenadas cartesianas.

2 Representa el cardioide r=6·(1 +cosα). Para ello utiliza una plantilla de hojas polares.

​​​​​​​CURIOSIDAD :

​​​​​​​​​El cardioide tiene por ecuacion r= a(1+cosα), es decir, r= a+a·cosα. Se trata de un caso particular de curvas que tienen como ecuación r= a+b·cosα. A esta curva se le conoce como limaçon o limacon.