
APROXIMACIÓN DE UNA RAÍZ CUADRADA
Estamos acabando el tema de radicales y en breve comenzaremos del de polinomios. Vamos a explicar como obtener una buena aproximación de la raíz cuadrada de un número fácilmente, relacionando ambos temas.
Esta actividad te servirá para desarrollar tu cálculo mental.
Para ello es conveniente recordar el cuadrado del mayor número posible de números que puedas. En 1ºESO, os recomendaba que os supieráis hasta el 20 al cuadrado. Por lo que puedes utilizar este método, en principio, para calcular las raices cuadradas de números inferiores a 400.
Empecemos:
Imagina que quieres calcular la raíz cuadrada del número n.
Lo primero que debemos saber és entre que dos cuadrados perfectos se encuentra.
Supongamos que a2 < n < b2
A continuación debemos saber si n se encuentra más cerca de a2 o b2. Ya que según de cual esté más cerca utilizaremos un procedimiento u otro (simplemente para obtener una mejor aproximación).
CASO 1: n está más cerca de a2
- Paso 1: calculamos n – a2
- Paso 2: dividimos el resultado obtenido entre 2a
- Paso 3: La aproximación de la raíz cuadrada de n es la suma de a más el resultado obtenido en el paso 2.
FÓRMULA:

CASO 2: n está más cerca de b2
- Paso 1: calculamos b2– n
- Paso 2: dividimos el resultado obtenido entre 2b
- Paso 3: La aproximación de la raíz cuadrada de n es la resta de b menos el resultado obtenido en el paso 2.
FÓRMULA:
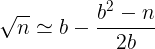
Pon en práctica estos procedimientos. Una vez hayas calculado la aproximación, calcula el resultado de la raíz con la calculadora y compara el resultado con tu aproximación.
DEDUCCIÓN DEL MÉTODO.
Para deducirlo necesitaremos utilizar las identidades notables: el cuadrado de la suma y el cuadrado de la diferencia.
CASO 1:
Partiremos de (a+x)2= a2+2ax+x2
Si despejamos el cuadrado del primer miembro obtenemos:
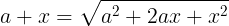
Si suprimimos el sumando x2, obtenemos la aproximación siguiente:

Si llamamos n= a2+2ax
Tenemos que:
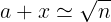
Despejando x de n= a2+2ax, se obtiene que:
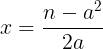
Luego:

CASO 2:
Partiremos de (b-x)2= b2-2bx+x2
Si despejamos el cuadrado del primer miembro obtenemos:
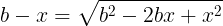
Si suprimimos el sumando x2, obtenemos la aproximación siguiente:
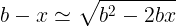
Si llamamos n =b2-2bx

Despejando x de n= b2-2bx, se obtiene que:
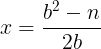
Luego:
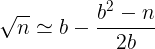


 Anterior
Anterior 

