
Aproximación de π
El cálculo del número π
En primer lugar os voy a demostrar como el número π está entre los números 3 y 4.
Para ello consideramos una circunferencia de radio R. Su longitud viene dada por la fórmula L=2πR
A continuación dibujaremos un cuadrado circuscrito a esa circunferencia como muestra la siguiente figura:
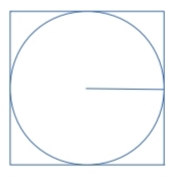
El cuadrado tiene de lado la longitud del diámetro de la circunferencia, es decir 2R. Si calculamos el perímetro tenemos que Pc= 4·2R
Como se ve en la figura la longitud de la circunferencia es menor que el perímetro del cuadrado, luego: L<Pc, es decir 2πR< 4·2R
A continuación consideramos el hexágono inscrito en la circunferencia.

Una de las propiedades que cumple es que la longitud del lado mide lo mismo que el radio. Por tanto, si calculamos el perímetro del hexágono tenemos que Ph= 6·R.
Como en la figura anterior, se ve que el perímetro del hexágono es menor que la longutud de la circunferencia, así pues se cumple que Ph<L, es decir 6R<2πR
Si tenemos en cuenta ambas desigualdades, se tiene que 6R<2πR< 4·2R.
Si simplificamos dividiendo las desigualdades entre 2R, obtenemos que 3<π< 4. que es lo que queriamos comprobar.
Este método fue utilizado por Arquímedes utilizando cada vez polígono de más lados hasta llegar a un de 96, obteniendo la siguiente aproximación: 3+10/71<π< 3+10/70, es decir, 223/71<π< 220/70=22/7.
Te puedes sentir como Arquímedes, calculando diferentes aproximaciones según el número de lados del polígono inscrito y circunscrito a una circunferencia en el siguiente enlace de la Red Educativa Digital Proyecto Descartes:
El día de Pi ya vimos que hubó un matemático y astrónomo llamado de Zu Chongzhi que obtuvo una aproximación racional de π: 355/113.
Pero es la de Arquímedes, 22/7, la que se utiliza para celebrar el día de la aproximación de π o casual pi day, el dia 22 de julio.
Más información sobre el número π: aquí
Sigue investigando sobre este número irracional y transcendente.


 Anterior
Anterior 
