El teorema de los 4 colores

El teorema de los 4 colores pertenece a la teoría de grafos. La tería de los grafos es una rama de las matemáticas y las ciencias de la computación.

El teorema nos asegura que cualquier mapa geográfico puede colorearse utilizando solo 4 colores.

Pero se deben tener en cuenta las siguientes consideraciones:

1. Han de ser regiones continuas. Hay paises que no cumplen este requisito como Estados Unidos en que Alaska esta separado del resto de los estados. 
2. Las fronteras no pueden compartir un único punto. En ese caso podrían tener el mismo color.

Este teorema nació como conjetura en 1852, y fue formulada por Francis Guthrie. Aunque no llegó a demostrarse hasta 1976 por Kenneth Appel y Wolfgang Haken. La novedad de esta demostración es que se utilizó por primera vez un ordenador para demostrar un teorema, lo que produjo un debate entre los matemáticos de la epoca.

El motivo que me ha llevado a hablaros de este teorema ha sido la entrada anterior en la que Mondrian usaba los colores primarios para realizar sus cuadros.

Es por ello que os planteo algunas actividades, para que pintéis los siguientes dibujos aplicando el teorema.

1. Dibujo abstracto. Usa los 4 colores que quieras.

Te dejo un modelo en el que he utilizado el amarillo, el azul, el blanco y el rojo. Si observas el dibujo verás que 2 regiones con un punto en común de frontera están pintadas de color rojo. Está permitido como indica una de las dos consideraciones que acepta el teorema.

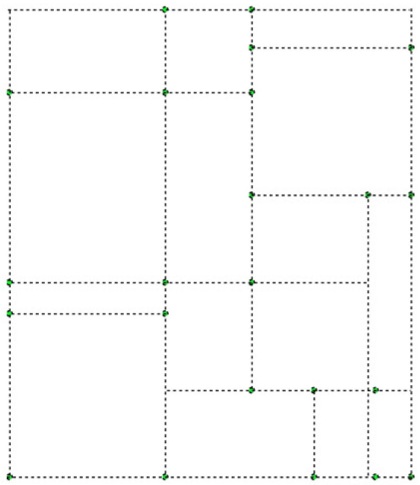
2. Plantilla Mondrian. En este caso, repasa de negro las líneas discontinuas y usa los colores amarillo, azul, blanco y rojo para que parezca un verdadero Mondrian.

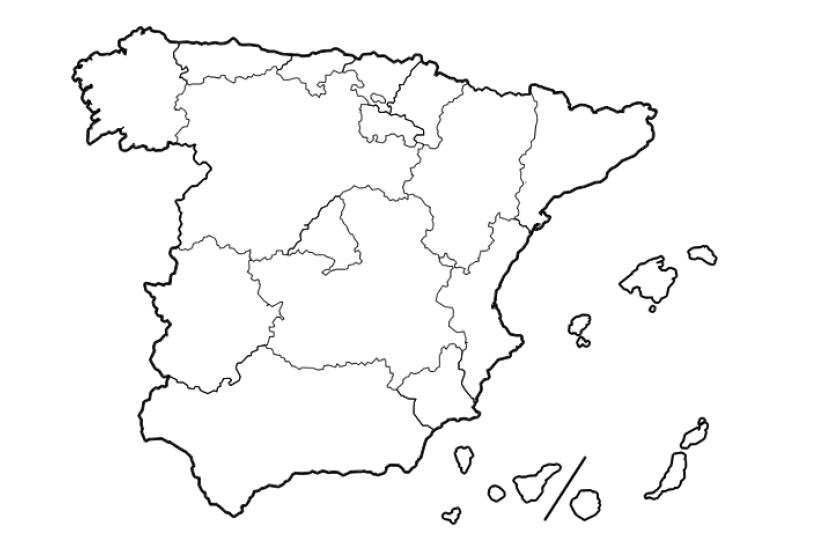
3. Mapa comunidades autónomas. Usa cuatro colores diferentes de tu elección.