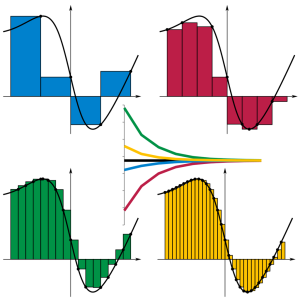
Sumas de Riemann

En esta entrada vamos a ver entender porque las áreas de las superficies se obtienen a partir de una integral definida.

Antes de todo vamos a recordar las definiciones de función derivada, primitiva, integral indefinida e integral definida que hemos visto en clase (bachillerato).

FUNCIÓN DERIVADA: Dada una función y=f(x), la función derivada y’=f'(x) se obtiene calculando:

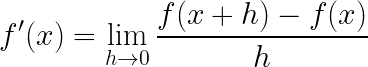
Se llama PRIMITIVA de una función y=f(x), a la función F(x) que cumple que F'(x)=f(x)

la INTEGRAL INDEFINIDA es el conjunto de todas las primitivas de una función, y se denota de la siguiente forma:

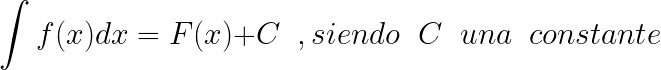
la INTEGRAL DEFINIDA es un número real. Se calcula la integral indefinida en un intervalo [a,b], siendo a y b los extremos de integración. Para calcularla, se utiliza la regla de Barrow:

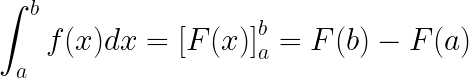
Una vez conocemos estos conceptos, pasamos a conocer las sumas de Riemann.

Supongamos que tenemos una función continua y queremos calcular el área que esta comprendida entre esa función, el eje x y las rectas x=a y x= b. (Nota: consideraremos el caso en el que la gráfica de esta función se encuentra sobre el eje X).

para que lo comprendáis mejor, lo vamos a ver sobre una función muy sencilla, la parábola y=x².

Supongamos que queremos calcular el área comprendida entre y=x², el eje x en el intervalo [1, 3].

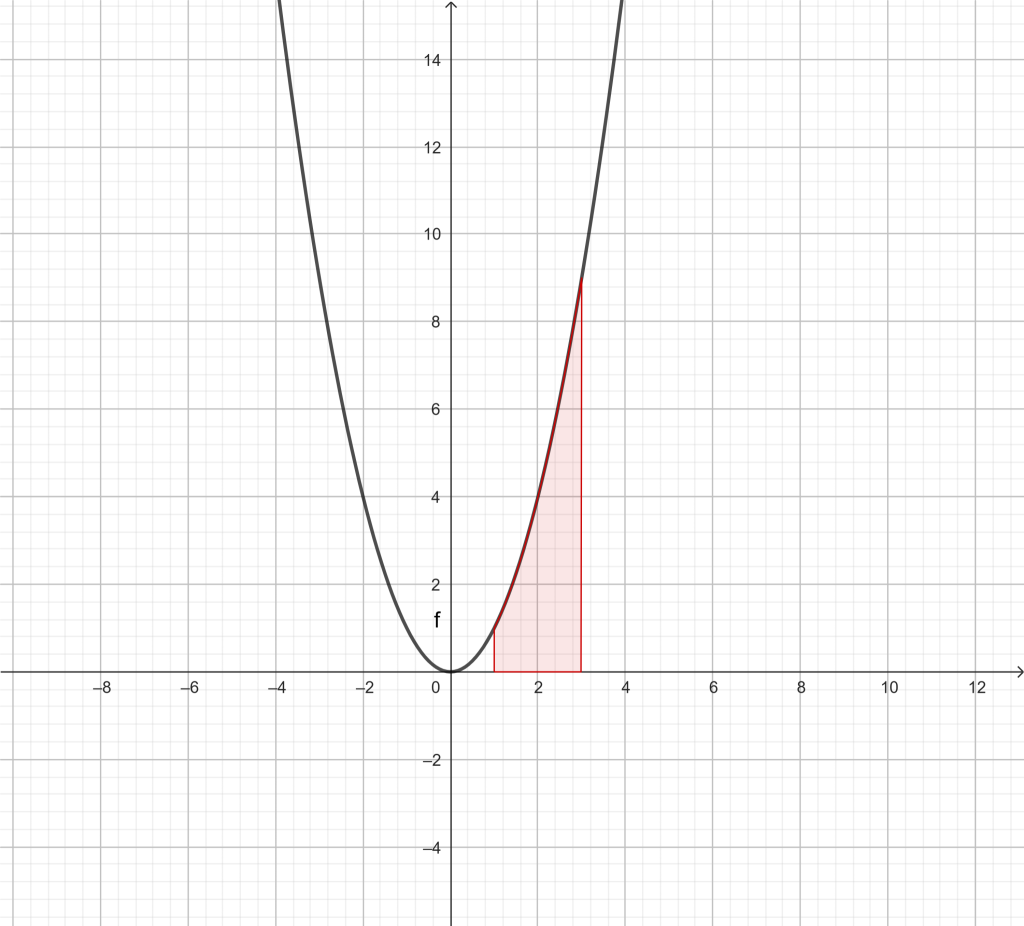
Para calcular el área, haremos una partición del intervalo [1, 3], por ejemplo x₀=1, x₁=2 y x₂= 3.

Calculamos la imagen de estos tres valores f(x₀)=f(1)=1, f(x₁)=f(2)=4 y f(x₂)= f(3)=9.

A continuación construimos rectángulos cuyas bases están formadas por los intervalos [1, 2] y [2, 3] considerando como altura la imagen del extremos inferior, como se observa en la figura:

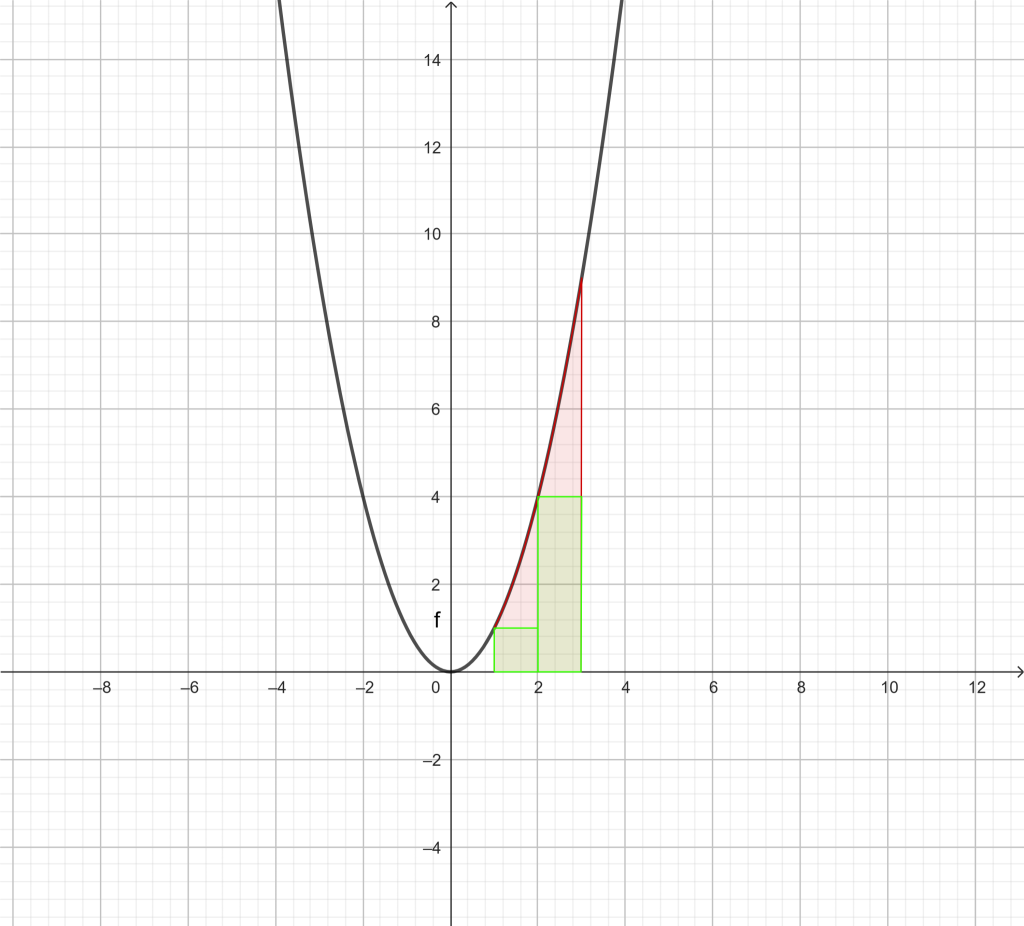
Como podéis observar, la suma de estos dos rectángulos es menor que el área que queremos calcular.

Si en vez de tomar como altura la imagen del extremo inferior, cogiéramos la del extremo superior, tendríamos que:

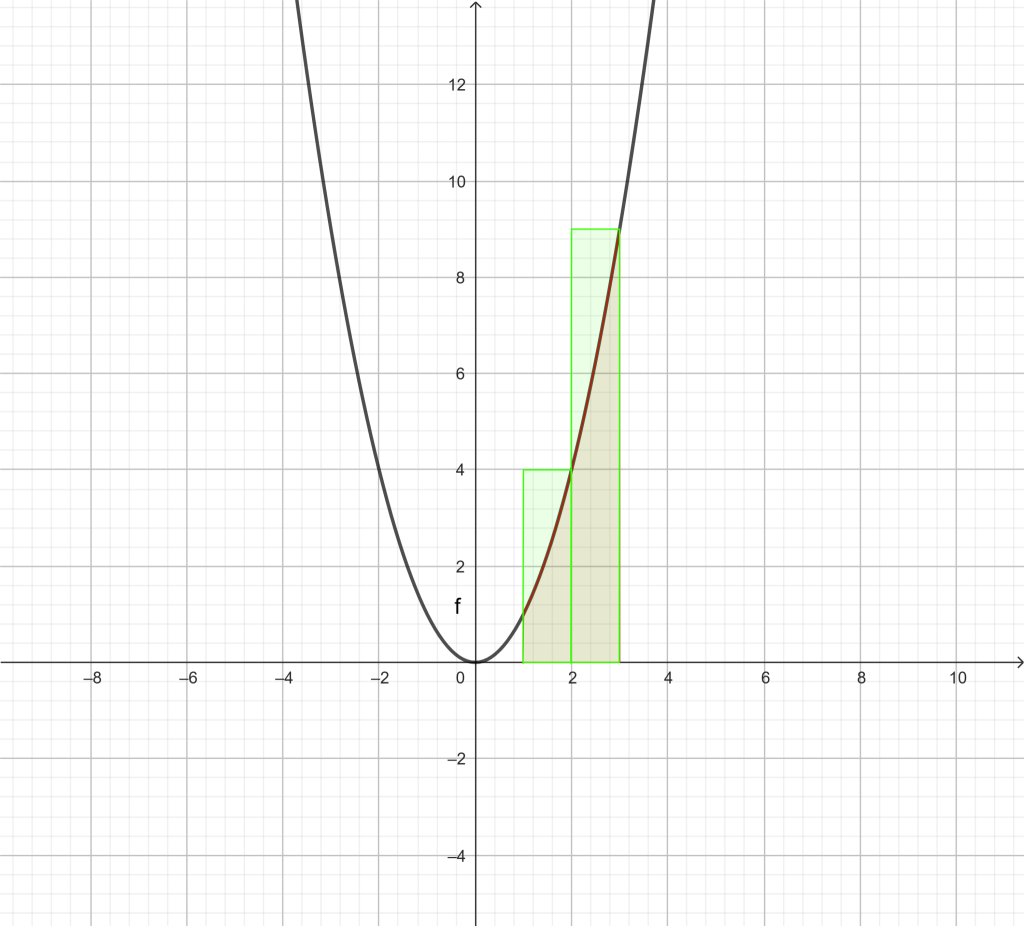
Se observa que en este caso, la suma del área de los rectángulos es mayor que la del área que queremos calcular.

Entonces, ¿Cómo podríamos aproximarnos al área deseada? Muy fácil, realizando una partición del intervalo más fina, es decir, que la amplitud del intervalo sea menor.

Así pues, vamos a pasar de una amplitud de 1 unidad a una amplitud de 0,5 unidades, y la partición del intervalo [1, 3] quedaría: x₀=1, x₁=1.5, x₂= 2, x₃=2.5 y x₄=3

Calculamos la imagen de estos tres valores f(x₀)=f(1)=1, f(x₁)=f(1.5)=2.25, f(x₂)=f(2)=4, f(x₃)=f(2.5)=6.25 y f(x₄)=f(3)=9.

Procedemos como antes, consideramos los rectángulos de bases los intervalos [1, 1.5], [1.5, 2], [2, 2.5], [2.5, 3] y cuya altura es la imagen del extremo izquierdo, y obtenemos

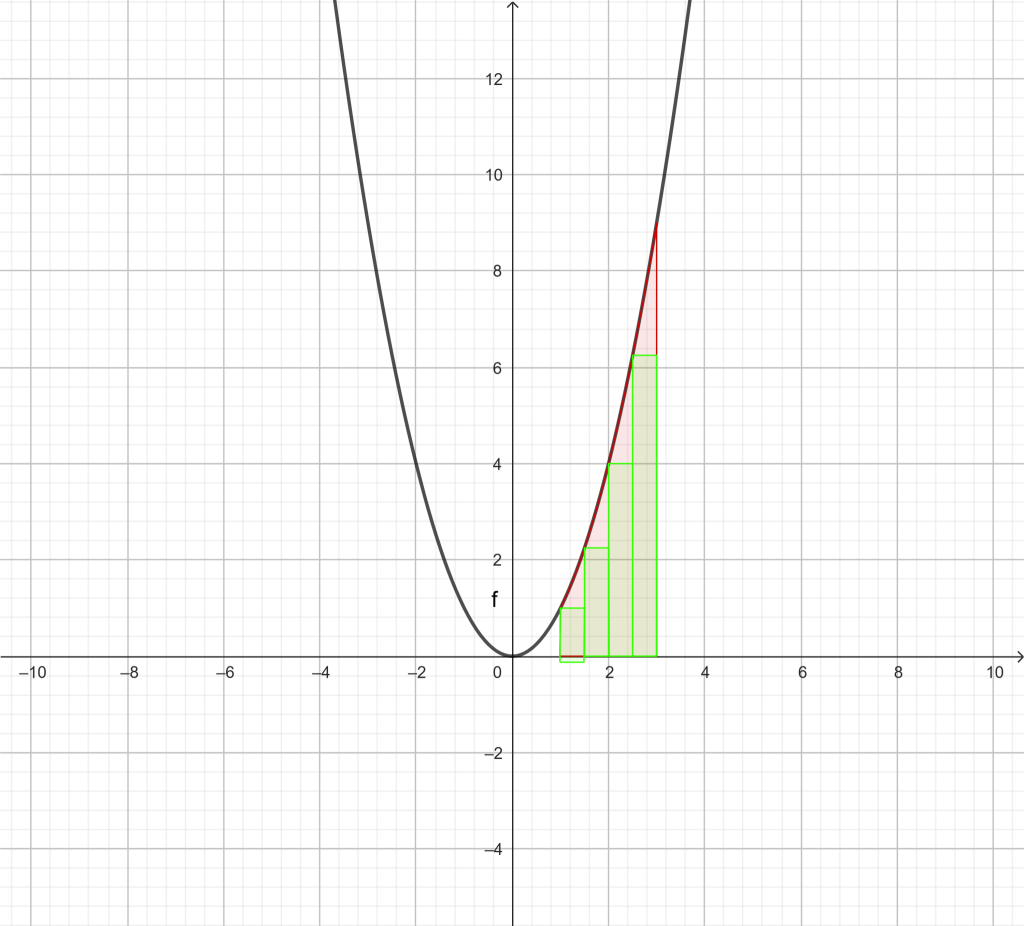
y si tomamos como altura la imagen del extremo derecho obtendríamos

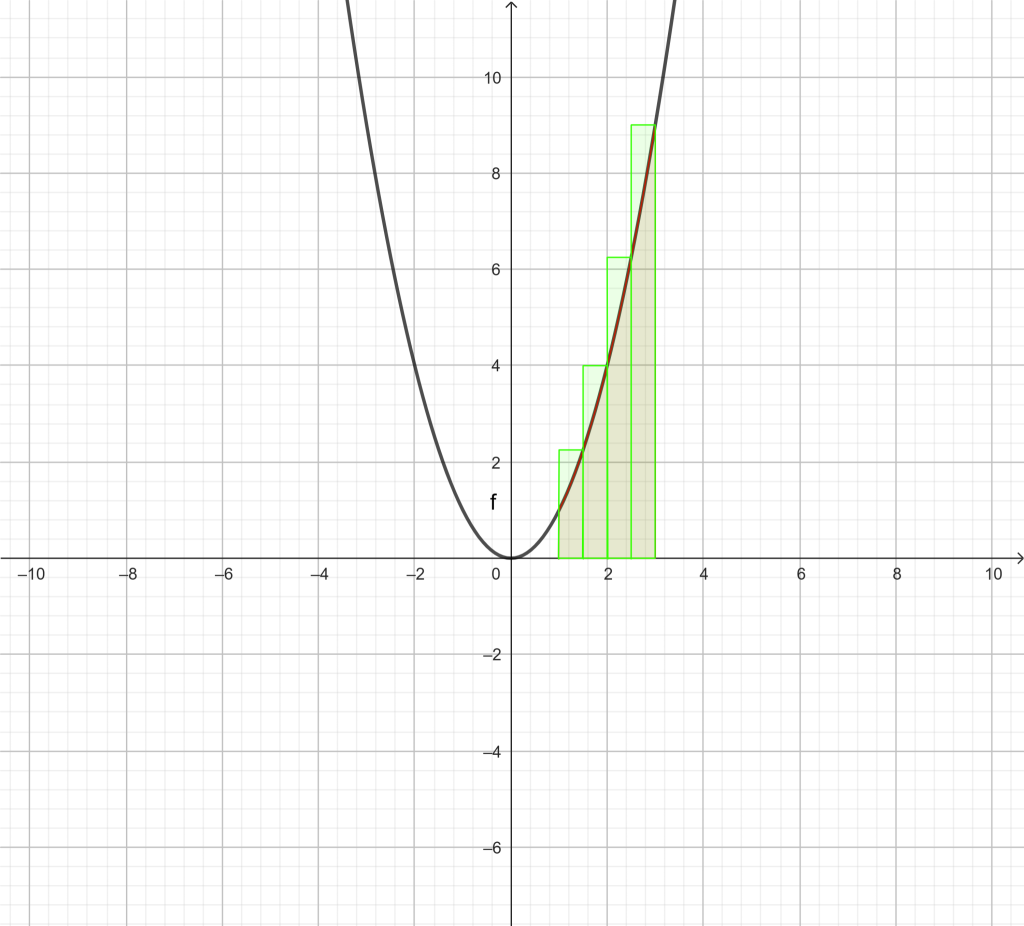
En este caso, la suma de las áreas de los rectángulos, bien sea por defecto o por exceso, se aproxima más al área que queremos calcular, pero aún no coincide.

Para que coincidiera, tendríamos que hacer que la amplitud del intervalo se redujera a cero, es decir, calcular el límite de las sumas de los rectángulos cuando la amplitud tienda acero. En ese caso, tanto la suma por defecto como la suma por exceso coincidirían y darían exactamente el valor del área que queremos calcular, que en este caso es la integral definida de y=x² entre 1 y 3.

Expresemos analíticamente lo que os acabo de explicar:

paso 1: AREA de y=x² entre 1 y 3:

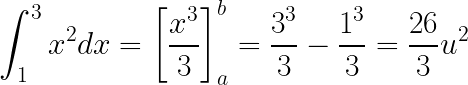
A= 26/3 = 8.6666… u²

Paso 2: Sumas de Riemann (área por defecto 1a partición)

s₁= (x₁-x₀)·f(x₀)+(x₂-x₁)·f(x₁)= (2-1)·f(1)+(3-2)·f(2)=1·1+1·4=5 u²

Paso 3: Sumas de Riemann (área por exceso 1a partición)

S₁= (x₁-x₀)·f(x₁)+(x₂-x₁)·f(x₂)= (2-1)·f(2)+(3-2)·f(3)=1·4+1·9=13 u²

Se verifica que s₁ < A < S₁, esto es 5 < 26/3 < 13

Paso 4: Sumas de Riemann (área por defecto 2a partición)

s₂= (x₁-x₀)·f(x₀)+(x₂-x₁)·f(x₁)+(x₃-x₂)·f(x₂)+(x₄-x₃)·f(x₃)= (1.5-1)·f(1) + (2-1.5)·f(1.5) + (2.5-2)·f(2) + (3-2.5)·f(2.5) = 0.5 · 1 + 0.5 · 2.25 + 0.5 · 4 + 0.5 · 6.25 = 6.75 u²

Paso 5: Sumas de Riemann (área por exceso 2a partición)

S₂= (x₁-x₀)·f(x₁)+(x₂-x₁)·f(x₂)+(x₃-x₂)·f(x₃)+(x₄-x₃)·f(x₄)= (1.5-1)·f(1.5) + (2-1.5)·f(2) + (2.5-2)·f(2.5) + (3-2.5)·f(3) = 0.5 · 2.25 + 0.5 · 4 + 0.5 · 6.25 + 0.5 · 9 = 10.75 u²

Se verifica que s₂ < A < S₂, esto es 6.75 < 26/3 < 10.75 y además los valores se aproximan más que en la primera partición al valor buscado que es 26/3= 8.6666…

Para acabar, veamos como se puede expresar de manera matemática este procedimiento:

En primer lugar definiremos las sumas inferior y superior de Riemann, que no es otra cosa que la suma de las áreas de estos rectángulos bien sea por defecto, bien sea por exceso.

Si tenemos la función y=f(x) definida en el intervalo [a, b] y una partición del intervalo en n partes, siendo x₀ =a, x₁ … , x_n =b y llamamos m_i  al valor de mínimo del intervalo [x_i, x_i+1] y M_i  al valor de máximo del intervalo, se define:

Suma inferior de Riemann a:

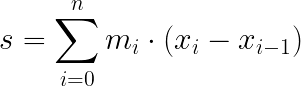
Suma superior de Riemann a:

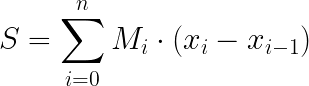
y se cumple que s < A < S, siendo A el área de la función y=f(x) en [a, b]

Conclusión:

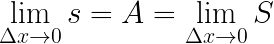
con